Моделирование фигурных чисел. Работа с “общим случаем”

При исследовании предметных и образовательных эффектов факультативного курса “Пифагорейское учение о числе и величине” было выдвинуто несколько предположений. Одно из них состояло в том, что факультативный курс “Пифагорейское учение о числе и величине” предоставляет детям новые ситуации для моделирования. Необходимо было проверить, действительно ли дети моделируют на новом материале.

Моделирование как учебное действие является центральным в учебной деятельности школьников на разных ступенях образования, поскольку без него невозможно теоретическое мышление.

В развивающем обучении, при изучении понятия числа, происходит моделирование процесса выделения кратного отношения и его результата [6]. Так, кратное отношение может быть выражено с помощью предметных или графических палочек (“меток”), указывающих результат как отдельного “наложения” меры, так и всех подобных “наложений” (сколько раз данная мера содержится в величине через их кратное отношение) (рис 3.1.).

Буквенная модель процесса и результат выделения кратного отношения выглядит так

В начальной школе при моделировании числа (как кратного отношения величин) объект моделирования и сама модель сильно не отличаются. Возникает вопрос, о том, что моделированием дети овладевают вообще или только на величинах.

Данный факультатив предоставляет детям новый материал для моделирования. А именно моделирование чисел представленных через эйдос, т.е. чисел которые представлены не как отношение величин (модель и объект моделирования существенно отличаются).

Были разработаны задания, решения которых связаны с построениями моделей фигурных чисел. В заданиях предлагалось доказать, что утверждения являются теоремами.

Рассмотрение и доказательство теорем есть ничто иное, как работа с фигурными числами в “общем случае”. Была выдвинута гипотеза о том, что за счет факультативного курса “Пифагорейское учение о числе и величине” дети научаются выстраивать способ работы с фигурными числами в “общем случае”.

Проведены проверочные занятия факультатива, где детям предлагалось решить данные задания.

На факультативе были пройдены теоремы:

№1. Сумма двух треугольных чисел равна гетеромекному числу;

№2. Сумма двух последовательных треугольных чисел равна квадратному числу.

На занятиях их рассматривали как задания, а не теоремы. Дети их решали (показывали) на конкретных примерах. Как теоремы не рассматривали и не доказывали.

Задание: доказать, что утверждения, ранее рассмотренные как задания, являются теоремами.

Ход занятия:

1. Дети раньше встречались с понятием теорема. Предстояло вспомнить, что теорема это утверждение, которое справедливо для всех чисел, и чтобы доказать, что утверждение является теоремой необходимо показать, что оно выполняется не только для конкретных чисел, а для любого взятого числа.

2. Доказательство теоремы №1.

а) Показать, что утверждение справедливо для конкретных чисел.

б) Построить модель треугольного числа (чтобы показать, что утверждение справедливо для всех треугольных чисел) (рис 3.2.).

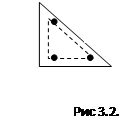выделить форму;

обозначить стороны;

выделить первый и последний гномон;

Прочее о педагогике:

Развитие навыков звукового анализа слова у детей дошкольного возраста в игровой деятельности
Формирование и развитие элементарных навыков письма и чтения является необходимой составной частью комплексной предшкольной подготовки детей. У дошкольников уже имеются некоторые представления об анализе и синтезе слов и графическом образе некоторых наиболее часто употребляемых букв русского языка. ...

Начальное и среднее образование
В рамках школьной программы учащиеся изучают как обязательные предметы (географию, историю, испанский язык, математику, искусство, музыку, естественные науки, так и предметы по выбору и основы профессиональной подготовки в какой-нибудь области). По завершении обязательного среднего образования (при ...

Содержание обучения на уроках окружающего мира, способствующего развития творческого мышления
Базой нашего исследования стала гимназия № 8 г. Коломна, 1 «В» класс. Эффективность развития творческих способностей во многом зависит от того материала, на основе которого составлено задание. На основе анализа психолого-педагогической и научно-методической литературы (Г.С.Альтшуллер, В.А.Бухвалов, ...