Реализация факультативного курса «Пифагорейское учение о числе и величине»

В общеобразовательном лицее №1 существует факультативный курс “Пифагорейское учение о числе и величине”, который проводится для детей третьего класса.

Факультативный курс “Пифагорейское учение о числе и величине” разработан и реализуется учителем математики общеобразовательного лицея №1 Ольшевской Н.А.

Данный факультативный курс проводится в общеобразовательном лицее №1 второй год, начиная с 2000-2001 учебного года.

Основная цель факультативного курса

Расширить знания о числе не только как о результате измерения величины меркой, но и представить число через эйдос (образ), подробно разработанный Пифагорейской школой.

Задействовать, за счет фигурного представления чисел, образное мышление школьников внутри математики.

Замысел факультативного курса

Дети знакомятся с новым представлением числа, которое существенно отличается от известного им представления числа как кратного отношения величин.

На факультативе дети впервые получают представление о понятии теорема. Убеждаются в том, что доказательства утверждений, теорем с помощью пифагорейских фигурных чисел являются наглядными (их можно увидеть собственными глазами).

Представление числа в виде эйдоса позволяет находить детям, без предварительных знаний (они являются очевидными), законы арифметических операций и различные числовые закономерности. Так, например дети занимаются построением очевидных арифметических прогрессий, хотя в начальных классах такую тему не проходят.

Детям предоставляется возможность написания реферативно-творческих работ по материалам древнегреческой математики.

Программа факультативного курса

1. Фигурные числа. (4 часа)

Эйдос (портрет) числа. Разновидности фигурных чисел. Гномоны (способы получения чисел). Идея квадратности, треугольности, гетеромекности чисел в Пифагорейском учении.

2. Учение о четных и нечетных числах. (12 часов)

Теорема как доказанное утверждение. Очевидность доказательства в древнегреческой математике. Четные и нечетные числа. Теоремы.

3. Правила построения квадратных, гетеромекных, прямоугольных, треугольных чисел. (10 часов)

Очевидные построения арифметических прогрессий. Теоремы о правилах построения различных чисел и случаи доказательства.

Содержание занятий факультативного курса

На занятиях факультатива дети знакомятся с разновидностями фигурных чисел. Изучают способ получения фигурных чисел при помощи гномона. Строят квадратные, треугольные, гетеромекные, прямоугольные и другие виды пифагорейских чисел. Решают различные задания, в которых необходимо построить, например квадратное число из двух последовательных треугольных чисел, гетеромекное число из двух одинаковых треугольных чисел и т.п.

При изучении четных и нечетных чисел дети решают задания, в которых нужно показать, что четное квадратное число делится на четыре равных квадратных числа или, что разность двух нечетных квадратных чисел может быть разделена на восемь одинаковых частей и т.п.

При изучении темы “Учение о четных и нечетных числах” дети знакомятся с понятием теоремы как доказанным утверждением. Могут убедиться в очевидности (наглядности) доказательства.

Некоторые основные теоремы о четных и нечетных числах

При доказательстве четное число изображается, как состоящее из двух равных половинок, а нечетное число составляется из четного числа и дополнительной единицы.

Теорема 1. Два четных числа составляют в сумме четное число (рис. 2.1.).

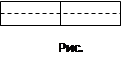
Теорема 2. Четное и нечетное числа в сумме составляют нечетное число (рис. 2.2.).

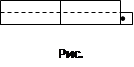
Теорема 3. Два нечетных числа в сумме составляют четное число (рис.2.3.).

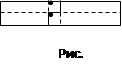
Теорема 4. Прямоугольное число, у которого хотя бы одна из сторон является четной, само является четным (число разделено на две одинаковые половины поперек четной стороны) (рис. 2.4.).

Теорема 5. Всякое гетеромекное число является четным. [В самом деле, одна из сторон гетеромекного числа обязательно будет четной, и тем самым (Теорема 4) всякое гетеромекное число является четным.] и т.д.

Изученные теоремы (правила) о четных и нечетных числах, дети могут использовать на уроках математики. В подтверждение этого был проведен эксперимент.

Эксперимент. На факультативном курсе были пройдены теоремы о четных и нечетных числах, при рассмотрении которых использовались фигурные числа. Спустя некоторое время была проведена проверочная работа, на которой детям предлагалось решить следующее задание:

Задание. Определите, не вычисляя, какое число четное или нечетное получится в результате вычислений.

а) 13205+787; б) 8025∙786;

13205+286; 8025∙137;

7438+568; 10378∙786.

7438+605.

Вопросы: №1. Почему вы считаете, что число четное или нечетное?

Прочее о педагогике:

Ансамбль песни и пляски Среднеазиатского военного округа
В 1969 году приказом Министерства обороны был сформирован Среднеазиатский военный округ. Через год в 1970 году в апреле месяце по приказу командующего округа генерала Лященко Н.Г. был сформирован Ансамбль песни и пляски Среднеазиатского военного округа (САВО). Первым художественным руководителем и ...

Исследование психологической диагностики учащихся
По методике мотивации учебной деятельности младших школьников Лускановой Н.Г. у учащихся было выявлено: Рисунок 3. Уровень школьной мотивации учащихся У 24% детей выявлен средний уровень школьной мотивации, учащиеся положительно относятся к школе, понимают учебный материал, внимательны при выполнен ...

Принципы и закономерности процесса обучения и их реализация в деятельности учителя
Общие образовательные закономерности: а) направленность образования на решение задач всестороннего и гармоничного развития личности; б) деятельностный характер обучения и воспитания; в) единство потребностно-мотивационной сферы и учебно-познавательной деятельности; г) проявление уважения и требоват ...