История развития понятия площади и ее измерения

S= р(р-а)(р-b)(р-с)(р-d)= (р-а)2(р-b)2=(р-а)(р-b)

так как а=с, b=d. Так как р-а=b, р-b=а, то получим S=аb.

Формула Брахмагупта верна не для любого четырехугольника. Она применима для равнобедренной трапеции и для вписанных в круг четырехугольников, диагонали которых взаимно перпендикулярны. Сам Брахмагупта был осторожен в применении своей формулы и пользовался ею только для определения площадей выше указанных фигур. Его формула, хоть и давала лишь приближенное значение истинного размера площади любого четырехугольника, облегчала измерение площадей земельных участков, так как обход участка по периметру и его измерение – задача несложная.

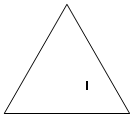
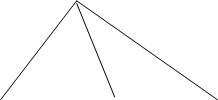
Задачи деления площадей фигур с помощью пересекающих их прямых и превращение одной фигуры в другую путем разрезания и пересоставления новых фигур из полученных частей заинтересовали греческих математиков, так как землемерие и архитектурные работы выдвигали задачи такого содержания. На рисунке видно деление пополам площади треугольника прямой, проходящей через одну из его вершин. Площадь треугольника разделяется медианой на две равные части, так как 1+2=1׳+2׳.

Одной из самых простых и удобных фигур для измерения площадей является квадрат.

2 2׳

1 1׳

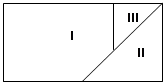
Поэтому математики издавна стремились превращать любую фигуру в равновеликий ей квадрат. Например, решали задачу о построении треугольника, равновеликого данному многоугольнику, и квадрата, равновеликого полученному треугольнику и т.д. Для решения аналогичных задач данный многоугольник разбивали на треугольники, так как всякий треугольник можно превратить в параллелограмм. При этом основание параллелограмма должно равняться основанию треугольника, а высота параллелограмма – половине высоты треугольника (рис. 6). Для этого достаточно провести среднюю линию треугольника.

II I III

Параллелограмм превращали в равновеликий ему прямоугольник, а прямоугольник в равновеликий ему квадрат.

Первые сведения об измерении площадей и расстояний на Руси относятся к XI веку. В Государственном Эрмитаже хранится камень с надписью: «В лето 6576 Глеб князь мерил морем по льду от Тмутороканя до Корчева 14 тысяч сажен». В этой записи говорится об измерении в 1068 году расстояния между городами Тамань и Керчь через Керченский пролив по льду.

Прочее о педагогике:

Методы изучения коллектива и личности, применяемые учителем в педагогической работе
Процессы воспитания, образования, обучения имеют коллективный (групповой) характер. Наиболее часто применяемые методы их изучения - массовые опросы участников данных процессов, проводимые по определенному плану. Эти вопросы могут быть устными (интервью) или письменными (анкетирование). Широко испол ...

Современные модели обогащения содержания образования
Современное российское образовательное законодательство не только допускает, но и прямо предполагает различные направления в педагогике и педагогической психологии и соответственно их реализацию в образовательных учреждениях. Существуют образовательные (педагогико-психологические) концепции, по кот ...

Содержание и методика развития координационных способностей
Младший школьный возраст является наиболее благоприятным для развития физических способностей В связи с этим одной из главных задач, которую мы решали на занятиях общей физической подготовки является, обеспечение разностороннего развития координационных (ориентирование в пространстве, быстрота и то ...