Пифагорейское учение о числе

Числа-произведения делились пифагорейцами на “прямолинейные”, т.е. простые числа, которые, так как они не разлагаются на множители, изображались точками, расположенными вдоль отрезка; “плоскостные числа”, разлагающиеся на два множителя и изображающиеся точками, образующими прямоугольник или квадрат, и “телесные числа”, разлагающиеся на три множителя и изображающиеся точками, образующими параллелепипед или куб.

Среди чисел-сумм пифагорейцы выделяли “многоугольные числа”. Наиболее простыми из них были “треугольные”:

1, 1+2=3, 1+2+3=6, 1+2+3+4=10,…

Из треугольных чисел пифагорейцы получали и все квадратные числа (рис. 1.7.).

Тем же путем, присоединяя, друг к другу три равных треугольных числа, получали пятиугольные числа и т.д.

Далее определялись “пирамидальные числа”, образуемые сложением многоугольных чисел. Простейшие из них, “четырехгранные числа”, получаются из треугольных чисел 1=1, 1+3=4, 1+3+6=10, 1+3+6+10=20… и изображаются в виде пирамид с треугольным основанием [12].

Представление числа в виде правильных геометрических фигур помогало пифагорейцам находить различные числовые закономерности.

Например, чтобы получить общее выражение для п-го треугольного числа, которое есть не что иное, как сумма п натуральных чисел 1+2+3+…+п, достаточно дополнить это число до прямоугольного числа п*(п+1) и увидеть (именно увидеть глазами) равенство:

1+2+3+…+п=п*(п+1) (рис 1.8.). (1)

Написав последовательность квадратных чисел, легко увидеть глазами выражение для суммы п нечетных чисел (рис. 1.9.):

1+3+5+…+(2п-1)= (2)

(При выводе равенства использован метод гномона.)

. … ….

… ….

… ….

….

Наконец, разбивая п-е пятиугольное число на три (п-1) треугольных (после чего остается еще п “камешков”), легко найти его общее выражение:

1+4+7+…+3п-2=п+3 (3)

Разбиением на треугольные числа получается и общая формула для п-го k-угольного числа

, (4)

откуда при k=2,3,4 следуют формулы (1-3).

Конечно, сегодняшний школьник легко заметит, что суммы (1-3) есть не что иное, как арифметические прогрессии, разность которых d соответственно равна 1,2,3 (для k-угольного числа d=k-2), и по соответствующей формуле найдет эти суммы и общую формулу (4):

Но в том-то и прелесть пифагорейских доказательств, что они не требуют никаких предварительных знаний и в буквальном смысле очевидны.

Фигурное представление чисел помогало пифагорейцам открывать законы арифметических операций.

Так, представляя плоское число 10 в двух формах (рис 1.10.):

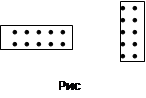
5*2=2*5=10,

легко “увидеть” переместительный закон умножения: ab=ba.

В том же числе 10:

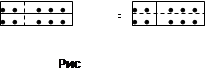
(2+3)*2=2*2+3*2=10

можно “разглядеть” и распределительный закон сложения относительно умножения (рис 1.11.):

(a+b)c=ac+bc и т.д

Фигурные числа (например, квадратные и кубические) дали возможность легко переходить к числовой характеристике геометрических объектов – измерению площадей и объемов, т.е. подойти к решению собственно геометрических задач.

Прочее о педагогике:

Двигательно-координационные способности и основы их воспитания
В современных условиях значительно увеличился объем деятельности, осуществляемой в вероятностных и неожиданно возникающих ситуациях, которая требует проявления находчивости, быстроты реакции, способности к концентрации и переключению внимания, пространственной, временной, динамической точности движ ...

Традиционная культура
Развитие культуры Российской Федерации основывается на фундаментальном значении отечественной культуры в жизни государства и общественного сознания как целостной системы ценностей, формирующей идентичность нации, единство Российского государства, влияющей на все сферы государственного и гражданског ...

Личностно-ориентированное взаимодействие
Педагогическое воздействие осуществляется педагогом с целью развития личности ребенка, перевода его на позицию субъекта. Педагогическое воздействие - это не любое воздействие, а воздействие педагога, являющегося носителем сознания, воли, отношений, а, следовательно, осознающим связи своего <Я> ...