Содержание и методика обобщающего повторения на примере темы: «Четырехугольники»

Можно не менять привычные учащимся избыточные определения, но обязательно подчеркнуть тот факт, что, чтобы убедиться, что рассматриваемый параллелограмм будет ромбом, достаточно проверить равенство двух смежных сторон, а чтобы убедиться, что он будет прямоугольником, достаточно доказать, что один из его углов прямой.

После этого отмечаем особые свойства диагоналей прямоугольника и ромба и опять ставим вопрос, будут ли эти условия не только необходимыми, но и достаточными, т. е. являются ли эти условия признаками рассматриваемых фигур. Как это проверить? Учащиеся должны сообразить, что для ответа на поставленный вопрос следует сформулировать и доказать теоремы, обратные к теоремам, выражающим свойства диагоналей прямоугольника и ромба.

Запишем одну из этих теорем.

Дано: АВСД - прямоугольник. Доказать: АС=ВД.

Обратное к этой теореме утверждение записывается так:

Дано: в четырёхугольнике АВСД АС=ВД .

Доказать: АВСД — прямоугольник.

Легко убедиться, что это утверждение несправедливо. Приведите примеры, подтверждающие этот факт. Учащиеся могут вспомнить, что диагонали равны у равнобочной трапеции, или начертить произвольный четырехугольник с равными диагоналями. Таким образом, мы убеждаемся, что равенство диагоналей не выделяет прямоугольник из класса четырехугольников (среди четырёхугольников с равными диагоналями есть и не являющиеся прямоугольниками).

Здесь учитель знакомит учащихся с еще одним способом получения утверждений, обратных данному. Замечает, что условие прямой теоремы может быть разбито на две части.

Дано: 1) АВСД — параллелограмм.

2)ÐА=900.

Доказать: АС = ВД.

Если теперь поменять местами заключение и вторую часть условия, то мы получим утверждение:

Дано: АВСД — параллелограмм

АС=ВД.

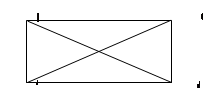Это утверждение легко доказать. Докажите самостоятельно.

Если учащиеся затрудняются, то можно "навести" их на мысль, обратив внимание, что ÐА + ÐД = 1800 (АВСД — параллелограмм ). Что осталось теперь доказать? (ÐА=ÐД).

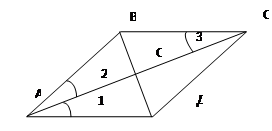Аналогичную работу проводим с установлением признаков ромба, основанных на свойствах его диагоналей. Вспоминаем теорему о свойствах диагоналей ромба.

Дано: АВСД — ромб.

Доказать: 1) ВД | АС;

2) ÐВАС =ÐСАД.

Для этой теоремы можно составить две обратные:

Теорема 1 Теорема 2

Дано: ВД | АС Дано: ÐВАС = ÐСАД

Доказать: АВСД — ромб. Доказать: АВСД — ромб.

Легко показать, что каждая из этих теорем несправедлива, приведя хотя бы по одному "контрпримеру";

Интересен вопрос. А как можно видоизменить первый чертеж чтобы его можно било использовать одновременно для "опровержения" и теоремы 1 и теоремы 2 (Достаточно взять АО=ОС и тогда ÐAВД=ÐДВС.

Используя второй способ образования обратных теорем, с которым учащиеся ознакомлены при установлении признака прямоугольника.

Имеем:

Прямая теорема: Дано:

Прочее о педагогике:

Причины искаженных взаимоотношений между педагогами и детьми
Владимир Набоков любил повторять, что детей надо баловать, ибо неизвестно, какая судьба их ждет. Это значит, что детей следует хвалить. И как можно чаще. Шанс же на похвалу нужно дать всем учащимся. Каждый ребенок достоин похвалы. Слабый он или сильный, задира или тихоня, красавчик или нет – он жде ...

Основные линии противоречий в социально-педагогическом процессе и причины возникновения конфликтов
Основными противоречиями и источниками конфликтов в этом процессе были и остаются проблемы, чему учить и как быть. Система образования как социальный институт взаимодействует со всеми сферами общественной жизни. Поэтому на макроуровне противоречия и конфликты в социально-педагогическом процессе воз ...

Педагогические технологии активизации обучения: общая характеристика, особенности
Термин «педагогическая технология» достаточно основательно закрепился в профессиональном сознании педагогов конца XX - начала XXI века. Можно уверенно говорить о том, что современные педагоги ведут профессиональные диалоги «на языке» педагогических технологий. На наш взгляд, для осмысления сущности ...