Содержание и методика обобщающего повторения на примере темы: «Четырехугольники»

Сообщается, что если (1)Þ(4), то утверждения называются эквивалентными. Аналогично эквивалентны утверждения (2) и (3) [(2)Û(3)].

Словами формулу (1)Þ(4) можно расшифровать так: если из условия А следует (вытекает) условие В, то без в нет и А (из нет в нет А), иными словами В необходимо для А (без В не будет и А).

А далее сообщаем, что необходимое условие дает нам свойство, а если условие не только необходимо, но и достаточно, то получаем признак.

Иными словами, чтобы получить свойство В какого-нибудь объекта А, достаточно доказать теорему АÞВ, а чтобы убедиться, что рассматриваемое свойство В является признаком, следует ещё доказать теорему ВÞА (обратную).

Вместе с учащимися вспоминаем все свойства параллелограмма и составляем таблицу.

Дано: АВСД – параллелограмм

Доказать: 1) АВ || СД

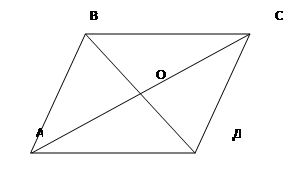ВС || АД

АВ = СД

ВС = АД

АО = ОС

ВО = ОД

ÐА = ÐС

ÐВ = ÐД

ÐА + ÐВ = 1800

ÐС + ÐВ = 1800

ÐС + ÐД = 1800

ÐА + ÐД = 1800

Обращаем внимание на тот факт, что каждое из условий 1–12 вытекает из того, что АВСД — параллелограмм, следовательно, каждое из них является необходимым условием того, чтобы четырехугольник АВСД был параллелограммом. Легко убедиться, что из каждого из условий 1–12 не следует, что АВСД — параллелограмм (например, если дано, что АВ II СД, что имеем трапецию, ибо ВС || АД).

Таким образом, каждое из условий 1–12, взятое в отдельности, признаком параллелограмма не является. Теперь начнём комбинировать свойства по два (Сколько таких комбинаций будет? Как сосчитать все комбинации, чтобы быть убеждённым, что ни одна не пропущена?). Убеждаемся, что некоторые из комбинаций дают признак параллелограмма. Какие из комбинаций по два дают известные уже вам признаки параллелограмма? [(1, 2), (1, 3), (2, 4), (5, 6)].

В то же время легко видеть, что не каждая из комбинаций по два дает признак параллелограмма. Например, из того что АВ II СД и ВС = АД следует, что фигура АВСД — равнобочная трапеция, а не параллелограмм.

Естественно встает вопрос, сколько же всего признаков у параллелограмма? Для ответа на этот вопрос нужно перебрать все возможные комбинации и либо доказать полученную теорему, либо привести пример, опровергающий её (контрпример). Ясно, что эта работа на уроке проделана быть не может. Она может быть дана в качестве индивидуальных заданий на дом хорошо успевающим учащимся, или еще лучше, предложена в качестве коллективной работы кружковцам. Здесь встают интересные вопросы о планировании работы, о разделении труда при решении этой проблемы, об организации самоконтроля и взаимоконтроля, о подведении окончательных итoгoв, т.e. вопросы, возникающие при организации любой трудовой деятельности.

Далее аналогичную работу можно провести по выяснению признаков прямоугольника и ромба. Но этой работе должно предшествовать уточнение определений прямоугольника и ромба. Действительно, достаточно потребовать, чтобы у параллелограмма был один прямой угол, т. к. из условия (АВСД — параллелограмм; ÐА=900) следует, что ÐВ=900, ÐС=900, ÐД=900. Для доказательства этого факта достаточно воспользоваться известными свойствами углов параллелограмма.

Аналогично, легко доказать теорему (АВСД — параллелограмм, АВ=ВСÞАВ=ВС=СД=АД), из которой следует, что ромбом называется параллелограмм, у которого две смежные стороны равны.

Прочее о педагогике:

Рекомендации по формированию вербального общения
Развитие и совершенствование навыков общения у умственно отсталого ребенка на разных этапах жизни - от рождения до взрослости — требует от педагогов, психологов и родителей много внимания и терпения. Родители и специалисты должны вести усиленное наблюдение за его поведенческими и речевыми реакциями ...

Развивающе-воспитательная функция
Уже подчеркивалось, что развивающе-воспитательная функция, пронизывает все функции учебника, что в условиях сегодняшней школы она является стержневой, ведущей во всем процессе создания учебника. Но именно поэтому в процессе исследования теоретических проблем школьного учебника есть необходимость ра ...

Анализ зарубежного и отечественного опыта работы по социально-педагогической поддержке младших школьников, обучающихся на дому
В развитых странах за рубежом уже сложились определенные стандарты, формы и методы работы по социально-педагогической поддержке младших школьников с ограниченными возможностями здоровья, обучающихся на дому. Во-первых, это максимально возможная интеграция ребенка с ограниченными способностями в общ ...