Содержание и методика обобщающего повторения на примере темы: «Четырехугольники»

АВСД –параллелограмм, АВ = ВС.

Доказать: ВД | АС

Обратная теорема:

Дано: АВСД –параллелограмм, ВД | АС.

Доказать: АВ=ВС

Вспоминая уточненное определение ромба, даем такую формулировку обратной теоремы: "Если в параллелограмме диагонали взаимоперпендикулярны, то этот параллелограмм — ромб".

Схема аналитического рассуждения при отыскании доказательства этой теоремы.

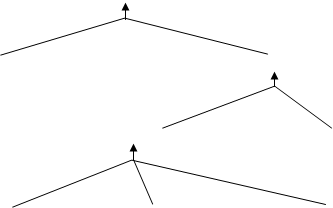АВСД – ромб

АВСД – параллелограмм АВ=ВС

DАВО = DСВО ÐАОВ = ÐСОВ

Ý ВД | АС

АО = ОС ВО – общая ÐАОВ = ÐСОВ

Ý

АВСД – параллелограмм ВД | АС

Аналогично формулируем второй признак ромба: "Если в параллелограмме диагональ делит угол пополам, то этот параллелограмм — ромб". Аналитическое рассуждение проводится аналогично.

Схематическая запись доказательства

АВСД — параллелограмм ÞАД II ВС Þ (Ð1 = Ð3, Ð1 = Ð2) Þ

ÞÐ2 = Ð3 Þ (АВ=BС, АВСД - параллелограмм) Þ АВСД — ромб.

Обобщая полученные результаты, полезно обратить внимание школьников на тот факт, что равенство диагоналей не выделяет прямоугольник из множества всех четырехугольников, но выделяет его из множества параллелограммов, и предложить им самостоятельно сформулировать аналогичные утверждения (их 2!) для ромба.

Для поверки того, владеют ли учащиеся признаками параллелограмма, ставим перед ними следующую проблему:

Как сформулировать признаки прямоугольника и ромба, основанные на свойствах их диагоналей, чтобы они выделяли прямоугольник и ромб из множества всех четырехугольников? Подсказка, если ученики не справляются: условие АВСД — параллелограмм, каким требованием относительно его диагоналей можно заменить.

Получаем признаки:

1. Если в четырехугольнике диагонали равны и точкой их пересечения делятся пополам, то этот четырехугольник — параллелограмм.

2. Если в четырехугольнике диагонали взаимноперпендикулярны и делятся точкой пересечения пополам, то этот четырехугольник — параллелограмм.

3. Признак формулируем аналогично.

Переходя к выяснению признаков квадрата, подчеркиваем, что квадрат является как частным случаем прямоугольника, так и ромба и следовательно обладает всеми свойствами прямоугольника и всеми свойствами ромба. Ставится проблема: выделить комбинации свойств диагоналей, которые выделяли квадрат из множества прямоугольников, из множества ромбов, их множества параллелограммов, из множества четырехугольников.

Если ученики осмыслили рассмотренный материал о признаках прямоугольника и ромба, то они легко ответят на поставленные вопросы и сформулируют следующие признаки квадрата:

Квадратом является:

Прямоугольник с взаимно–перпендикулярными диагоналями,

Прямоугольник, у которого диагональ делит угол пополам.

Ромб с равными диагоналями.

Параллелограмм, у которого диагонали равны и взаимно–перпендикулярны.

Параллелограмм, у которого диагонали рваны и делят угол пополам.

Четырехугольник, у которого диагонали равны, взаимно–перпендикулярны и в точке пересечения делятся пополам.

После этого можно перейти к решению задач, требующих применения изученных признаков.

Прочее о педагогике:

Пути коррекции возможных нарушения поведения учащихся с задержкой психического развития
Поведенческая коррекция признается одной из наиболее адекватных и эффективных форм психологического воздействия на личность с отклоняющимся поведением. Отклоняющееся поведение имеет место постольку, поскольку работают механизмы его сознательной и бессознательной мотивации. Человек с девиантным пове ...

Требования к игрушке
Основное требование к игрушкам определила Н.К. Крупская в статье «Об игрушках для дошколят»: игрушка должна содействовать развитию ребёнка на каждой возрастной ступеньке дошкольного детства. Малышу нужны свои игрушки, которые помогут ориентироваться в окружающем мире, будут стимулировать его самост ...

Методические рекомендации по декоративному рисованию в старшей группе
В старшей группе в качестве композиционного приема чаще применяют принцип чередования элементов, что делает узор более декоративным. Чередование может включать 2-3 элемента, различных по форме или цвету. В качестве элементов узора дети учатся использовать разнообразные линейные формы (толстые и тон ...