Содержание и методика обобщающего повторения на примере темы: «Четырехугольники»

Нетрудно показать, что точка М является серединой АВ1. В самом деле, длины отрезков АА1 и ВВ1 равны 1/2ДС, а сами отрезки || ДС.

Поэтому четырехугольник А1АВ1В является параллелограммом. Точка М — середина его диагонали АВ. Поэтому М принадлежит диагонали А1В1 и является ее серединой.

Итак, в D NA1B1 известны стороны NA1, В1N и заключённая между ними медиана. Для того, чтобы построить этот треугольник, отметим точку N1, симметрично относительно М. Очевидно, |АN| = |В1N|.

Треугольник N1NA1 можно построить по трем известным сторонам: |NA1| = |ДА|, |A1N1| = |В1N| = |CB| и |NM1| = 2|NM|.

Теперь построим искомый четырехугольник. Делим отрезок N1N точкой М на два конгруэнтных отрезка, строим точку В1, симметричную А1 относительно М. По трем сторонам построим треугольники А1МА и МВВ1. Перенеся отрезок А1А на вектор А1N, а отрезок ВВ1 на вектор В1N, подучим все четыре вершины искомого 4-х угольника АВСД. Нетрудно показать единственность решения задачи.

Усилению развивающих функций задачи способствует последующая постановка задач-аналогов, при решении которых используется некоторый(один и тот же) прием, основанный на применении определённого метода. Так как параллельный перенос элементов фигуры(АС) приводит к построению вспомогательного четырехугольника СВВ1Д1 с весьма интересными свойствами.

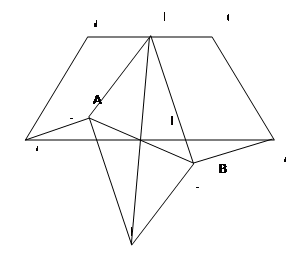Например, 4‑х угольник ДД1В1В — параллелограмм, стороны которого конгруэнтны диагоналям 4-х угольника АВСД, в углы конгруэнтны углами между этими диагоналями; длины диагоналей ДД1В1В вдвое больше длин отрезков, соединяющих середины противоположных сторон АВСД; расстояния от точки С до вершин этого параллелограмма равны соответственно длинам сторон 4-х угольника АВСД и т.д.

Многие в этих свойств позволяют решить задачи, аналогичные исходной, создают условия для распространения определенного приема на целый класс задач, способствуя, т.о., формированию у учащихся способностей к обобщению (через анализ).

Таковы, например, следующие задачи:

Задача 3. В четырехугольнике АВСД известны длина отрезка М, соединяющего середины сторон АВ и СД, длина диагонали АС и длины сторон АВ, ВС и АД.

Является ли данная фигура жесткой?

Задача 4. Построить трапецию АВСД по данным диагоналям АС, ВД, стороне АД и отрезу МN, соединяющему середины её оснований.

Рассмотрение этого примера показывает, как достаточно широко можно использовать обучающие, развивающие и воспитывающие функции задач в их единстве. В самом деле, в ходе решения этих задач используются различные свойства геометрических фигур, активно работает метод параллельного переноса и прием построения вспомогательной фигуры с весьма интересными свойствами, тесно связанными со свойствами заданной (искомой) фигуры (реализуются различные развивающие функции), задача легко моделируется (дотекает опытные решения), возбуждает интерес школьников (реализуются воспитывающие функции). Задача такова, что может служить источником разнообразных аналогичных задач, многие из которых как показал опыт, успешно составляются самими школьниками, что способствует формированию у них творческой активности.

Прочее о педагогике:

Игровые технологии, их роль и место в обучении профессиональному иноязычному общению
Игра, как приема обучения, есть действенный инструмент управления учебной деятельностью (деятельностью по овладению иноязычным общением), активизирующий мыслительную деятельность обучающихся, позволяющий сделать учебный процесс захватывающим и интересным. По мнению Д.Б. Эльконина, «человеческая игр ...

История развития понятия площади и ее измерения
Зарождение геометрических знаний, связанных с измерением площадей, теряется в глубине тысячелетий. Еще 4 – 5 тыс. лет назад вавилоняне вычисляли площади земельных участков, имеющих форму прямоугольника и трапеции, в квадратных единицах. Единицей измерения площади издревле использовали квадрат, так ...

Проектирование по дисциплине «Технология»
Цели новой образовательной области «Технология» будут достигнуты, если учащиеся получат возможность в процессе её освоения испытать себя выполнением ряда творческих практических работ, которые включают усвоение информации, овладение рабочими приемами, технологическими операциями и, что не менее важ ...