Содержание и методика обобщающего повторения на примере темы: «Четырехугольники»

Для приведения в систему материала по теме "Параллелограмм и его виды» очень хороша задача: «Определить вид четырехугольника, который получится, если последовательно соединить отрезками прямых середины сторон произвольного четырехугольника».

После доказательства того факта, что полученный четырехугольник будет параллелограммом, ставится вопрос: «Каким должен быть исходный четырехугольник, чтобы полученный оказался прямоугольником, ромбом, квадратом?».

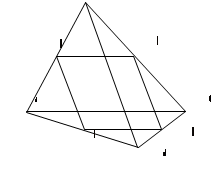Начертим произвольный четырехугольник.

В

Найдём середины сторон и изобразим схематично на чертеже равенство отрезков.

Соединим последовательно полученные точки E, F, M, N.

Вопрос: какой четырехугольник получился?

У разных учащихся ответ будет различным: параллелограмм, прямоугольник, ромб, квадрат. Учитель обращает внимание на то, что прямоугольник, ромб, квадрат — частные виды параллелограмма, поэтому всем придется доказывать, что четырехугольник EFMN — параллелограмм.

Дано: АЕ = ЕB, BF=FC, СМ=МД, ДN=NА.

Доказать: EFMN — параллелограмм.

Проводится анализ:

Вопрос: Для того, чтобы доказать, что EFMN — параллелограмм, что достаточно доказать?

Ответ; параллельность прямых EF и MN, а также ЕN и MF.

Вопрос: Как можно доказать? (или, если не отвечают: Используя какой признак параллельности прямых можно это доказать?).

Ответ: Первый признак параллельности прямых т.к. в других признаках участвуют углы, а в условии задачи об углах ничего не сказано.

Вопрос: В первом признаке параллельности прямых говорятся о трех прямых. Где взять третью прямую?

Ответ: Соединить точки А и С. Получим два треугольника — АВС и АДС.

Вопрос: Какое соотношение известно в этих треугольниках? Или: Чем являются ЕF и MN в DАВС и DАДС?

Ответ; ЕF является средней линией DАВС, ибо АЕ = FВ и ВГ = FC, а MN является средней линией DАДС, т.к. СМ = МД и ДN = NА.

Вопрос: Какой признак средней линии мы знаем?

Ответ: Средняя линия параллельна основанию.

Вопрос: Какой вывод можно сделать о ЕF и MN?

Ответ: ЕF || АС и МN || АС. Значит, по первому признаку параллельности прямых следует, что ЕF || MN.

Аналогично доказывается, что ЕN || FM.

Проведем так называемый «взгляд назад» и попробуем найти другое решение, более рациональное и короткое.

Вопрос: Как еще можно доказать, что четырехугольник EFMN — параллелограмм?

Или: Каким признаком параллелограмма можно воспользоваться, чтобы доказать, что четырехугольник EFMN — параллелограмм?

Ответ: Воспользоваться признаком параллелограмма, который заключается в том, что если в четырехугольнике противоположные стороны попарно параллельны и равны, то этот четырехугольник — параллелограмм. Значит надо доказать, что EF || MN и EF = MN.

Вопрос: Параллельность прямых EF и MN доказывается так, как это было сделано выше. Как доказать равенство ЕF и МN? или: Какое свойство средней линии мы знаем?

Ответ: Так как ЕF — средняя линия DАВС, то ЕF равна половине основания АС; MN средняя линия АДС и М равна половине основания АС. Значит ЕF = MN.

Это решение является более рациональным и коротким.

Теперь надо записать решение задачи. Для этого уже используется синтез.

Прочее о педагогике:

Перевод одних единиц физической величины в другие
Задача 7. Вычислите массу 2 л 30,74%-ного раствора азотной кислоты. По справочнику находим плотность данного раствора кислоты: 1,185 г/мл. Мы видим, что плотность и обьём заданы в различных единицах. Какие единицы выбрать: литры или миллилитры? Рассмотрим ситуацию приведения к меньшим единицам, к м ...

Особенности развития личности в подростковом возрасте
Для развития человека важен каждый возраст. И все же подростковый возраст занимает особое место в психологии. Подростковый - это самый трудный в сложный из всех детских возрастов, представляющий собой период становления личности. Главное содержание подросткового возраста доставляет его переход от д ...

Военно-патриотическое и культурное воспитание подростков и военнослужащих
Каждый человек отличается большой любовью к своей Родине — государству трудящихся и выражают эту любовь в конкретных делах, направленных на укрепление ее славы и могущества. Настоящих патриотов нашей Родины отличает последовательный интернационализм, т. е. глубокое уважение к другим странам, нашим ...