Площадь плоской фигуры и ее измерение

Эти треугольники равны. Площадь каждого из них равна

где - сторона правильного -угольника . Тогда площадь многоугольника равна

но . Следовательно,

Если -произвольный многоугольник, то его площадь находят, разбивая многоугольник на треугольники (или другие фигуры, для которых известны правила вычисления площади). В связи с этим возникает вопрос: если один и тот же многоугольник по-разному разбить на части и найти их площади, то будут ли полученные суммы площадей частей многоугольника одинаковыми? Доказано, что условиями, сформулированными в определении площади, площадь всякого многоугольника определена однозначно.

Кроме равенства и равновеликости фигур в геометрии рассматривают отношение равносоставленности. С ним связаны важные свойства фигур.

Многоугольники и называются равносоставленными, если их можно разбить на соответственно равные части.

Например, равносоставлены параллелограмм и прямоугольник (рис.3), так как параллелограмм состоит из фигур и , а прямоугольник – из фигур и , причем .

Нетрудно убедиться в том, что равносоставленные фигуры равновелики.

Венгерским математиком Ф.Бойяи и немецким любителем математики П.Гервином была доказана теорема: любые два многоугольника равносоставлены. Другими словами, если два многоугольника имеют равные площади, то их всегда можно представить состоящими из попарно равных частей.

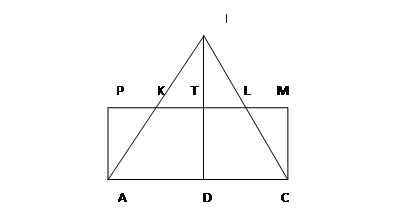
Рис. 4

Теорема Бойяни - Гервина служит теоретической базой для решения задач на перекраивание фигур: одну разрезать на части и сложить из нее другую. Оказывается, что если данные фигуры многоугольные и имеют одинаковые площади, то задача непременно разрешима.

Доказательство теоремы Бойяи-Гервина достаточно сложное. Мы докажем только утверждение о том, что всякий треугольник равносоставлен с некоторым прямоугольником, т.е. всякий треугольник можно перекроить в равновеликий ему прямоугольник.

Пусть дан треугольник (рис.4). Проведем в нем высоту и среднюю линию . Построим прямоугольник, одной стороной которого является , а другая лежит на прямой . Так как пары треугольников и , а также и равны, то треугольник и прямоугольник равносоставлены.

Мы выяснили, что вычисление площади многоугольника сводится по существу к вычислению площадей треугольников, на которые можно разбить этот многоугольник. А как находить площадь произвольной плоской фигуры? И что представляет собой число, выражающее эту площадь?

Прочее о педагогике:

Влияние мотивации на овладение иноязычной речевой деятельностью
Повышение мотивации обучающихся к учебной деятельности – один из актуальных вопросов дидактики. Реальным способом поддержания познавательных мотивов является «включение деятельности по овладению иностранным языком в деятельность, имеющую для учащихся определенной личностный смысл (игра, общение, тр ...

Высшее образование
Бакалавриат охватывает 2 курса (как правило, предоставляется возможность подготовки в Университет по гуманитарным предметам, социальным наукам). После прохождения бакалавриата, студенты могут поступать в Университет. Следует иметь в виду, что в некоторых Университетах недостаточно подобной двухгоди ...

Влияние развития мелкой моторики рук на развитие речи ребёнка
Подражание движениям рук, игры с пальцами стимулируют, ускоряют процесс речевого и умственного развития ребенка. Об этом свидетельствуют не только опыт и знания многих поколений, но и исследования физиологов, которые доказали, что двигательные импульсы пальцев рук влияют на формирование «речевых» з ...