Площадь плоской фигуры и ее измерение

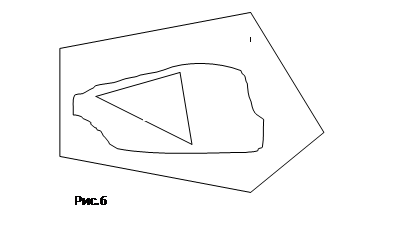
Пусть - произвольная плоская фигура. В геометрии считают, что она имеет площадь , если выполняются следующие условия: существуют многоугольные фигуры, которые содержатся в (назовем их объемлющими); существуют многоугольные фигуры, которые содержаться в (назовем их входящими); площадь этих многоугольных фигур как угодно мало отличаются от . Поясним эти положения. На рисунке 6 показано, что фигура содержит фигуру , т.е. -объемлющая фигура, а фигура содержится в , т.е. - входящая фигура. На теоретико-множественном языке это означает, что и, следовательно, можно записать, что

Если разность площадей объемлющей и входящей фигур может стать как угодно малой, то как установлено в математике, существует единственное число , удовлетворяющее неравенству для любых многоугольных фигур и . Данное число и считают площадью фигуры .

Этими теоретическими положениями пользуются, например, когда выводят формулу площади круга. Для этого в круг радиуса вписывают правильный -угольник , а около окружности описывают правильный -угольник . Если обозначить символами и площади этих многоугольников, то будем иметь, что , причем при возрастании числа сторон вписанных и описанных многоугольников площади будут увеличиваться, оставаясь при этом меньше площади круга, а площади будут уменьшаться, но оставаться больше площади круга.

Площадь правильного -угольника равна половине произведения его периметра на радиус вписанной в него окружности. При возрастании числа его сторон периметр стремится к длине окружности , а площадь - к площади круга. Поэтому

Для приближенного измерения площадей плоских фигур можно использовать различные приборы, в частности, палетку.

Палетка- это прозрачная пластина, на которой нанесена сеть квадратов. Сторона квадрата принимается за 1, и чем меньше эта сторона, тем точнее можно измерить площадь фигуры.

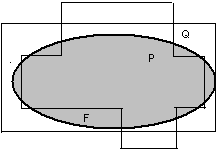
Накладываем палетку на данную фигуру . Квадраты, которые целиком лежат внутри , образуют многоугольную фигуру ; квадраты, имеющие с фигурой общие точки и лежащие внутри фигуры , образуют многоугольную фигуру (рис.7). Площади и находят простым подсчетом квадратов. За приближенное значение площади фигуры принимается среднее арифметическое найденных площадей:

Прочее о педагогике:

Сексуальное образование в школах
Сексуальное образование должно быть частью школьного учебного плана и должно начинаться как можно раньше. Основная цель такого образования – научить молодых людей быть ответственными за свое сексуальное поведение. Несмотря на то, что подростки указывают на своих сверстников и средства массовой инфо ...

Коррекция звукослогового анализа и синтеза у младших школьников с фонетико-фонематическим недоразвитием речи
Система обучения детей младшего школьного возраста с ФФНР включает коррекцию звукопроизношения, формирование фонематического восприятия, подготовку к обучению грамоте (Г.А.Каше, Т.Б.Филичёва, Г.В. Туманова). Коррекционное обучение также предусматривает овладение ребёнком на данном возрастном этапе ...

История возникновения военных ансамблей песни и пляски
Основой военных плясок является народно-сценический танец. Искусство народного танца - одно из древнейших. У каждого народа сложились свои танцевальные традиции, свой хореографический язык и пластическая выразительность. У каждого народа есть свой, наиболее характерный для него танец, в котором отр ...