Нахождение решений алгебраических и трансцендентных уравнений

Приближенное нахождение значений иррациональных чисел, нахождение решения алгебраических и трансцендентных уравнений – это задача теории чисел. При решении этой задачи необходимо оценивать точность приближения, в результате развивается аппарат, связанный с погрешностью.

Умение оперировать с приближенными числами дает возможность для приближенного решения уравнений (алгебраических и трансцендентных). В пособии алгебраическим называют комплексное или действительное число x0, удовлетворяющее уравнению вида

,

где числа a0, a1, …, an целые, и не все равны нулю, а n – натуральное. Всякое действительное или комплексное число, не являющееся алгебраическим, называется трансцендентным.

При нахождении решений алгебраических и трансцендентных уравнений решается две общих задачи:

1) получить метод, дающий возможность улучшить приближения;

2) получить приближенное решение с заранее заданной степенью точности.

В различают методы для нахождения приближенных корней алгебраических и трансцендентных уравнений.

Нахождение корней алгебраического уравнения

Для приближенного нахождения корней алгебраического уравнения нужно по правилу Декарта определить число положительных и отрицательных корней, после отделить их. Отделив корень, мы получаем возможность, в качестве его приближенного значения взять любое число из выделенного отрезка.

Отделение действительных корней уравнения F(x) = 0 очень удобно производить графически. Значения действительных корней уравнения F(x) = 0 являются абсциссами точек пересечения графика функции y = f(x) с осью Ox. Чтобы указать отрезки, заключающие только по одному корню уравнения, не требуется особой точности.

Для улучшения приближения корней алгебраического уравнения используют четыре способа:

Способ 1. Способ Ньютона (способ касательных).

В этом способе приближенное значение действительного корня улучшается по формуле

= – .

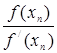Корень необходимо отделить, т. е. определить отрезок [a,b], в котором находится единственный действительный корень. За первое приближение корня следует взять значение того конца этого отрезка, на котором знак функции совпадает со знаком ее второй производной.

Например, найдем корень уравнения х2 – х – 1 = 0. Действительный корень находится на отрезке.

= 3 - ;

= 2; - ;

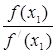= 5/3.

Способ 2.Способ линейной интерполяции (способ хорд).

Для вычисления (n + 1) – го приближения корня пользуются формулой

=

Заметим, что хn и хi - значения, между которыми находится искомый корень. За первое приближение корня можно принять значение любого из концов отрезка, на котором находится отделенный корень.

Способ 3. Служит для определения приближенного значения наибольшего и наименьшего по абсолютной величине корня алгебраического уравнения.

Если дано уравнение , то простой, наибольший по абсолютной величине корень можно приближенно найти из уравнения . Приближенное значение меньшего по абсолютной величине корня можно найти из уравнения .

Например,.

1) – 1 = 0, = 1 приближенный больший по абсолютной величине корень.

Прочее о педагогике:

Цели использования НИТ в системе образования
Выделим педагогические цели использования НИТ в системе образования: − интенсификация всех уровней учебной подготовки; − развитие личности обучаемого; −подготовка к жизни в условиях информационного общества; − реализация социального заказа, обусловленного процессами информат ...

Возможности реализации компетентностного подхода в преподавании истории государства и права в юридическом вузе
Происходящая в нашей стране модернизация образования, в том числе и высшего профессионального, стимулирует поиск новых путей обновления образовательной системы в соответствии со сложившимися общественными реалиями. Одним из основных направлений педагогической мысли, которое нацелено на внесение сущ ...

Психолого-педагогическая характеристика детей с ЗПР
В середине 20 века вследствие усложнения программ общеобразовательных школ, появилось большое количество детей, испытывающих трудности в обучении. Довольно часто таких детей отправляли во вспомогательные школы (для уо). Однако при медицинском обследовании у многих детей не обнаруживались специфичес ...