Нахождение решений алгебраических и трансцендентных уравнений

Для отрезка значения функции имеют разные знаки. В самом деле,

12 - 1 - 1 = -1;

1.52 – 1.5 – 1 = -0.25;

22 – 2 – 1 = 1;

2) z2 = (1.5 + 2)/2 = 1.75;

Получили два отрезка.

Для отрезка значения функции имеют разные знаки. В самом деле,

1.52 – 1.5 – 1 = -0.25;

1.752 – 1.75 – 1 = 0.3125;

22 – 2 – 1 = 1.

Таким образом, корень расположен на промежутке. Продолжая процесс можно найти корень с некоторой заданной степенью точности.

Нахождение корней трансцендентных уравнений

При решении трансцендентных уравнений необходимо уравнение F(х) = 0 представить в виде j(х) = y(х). После используют два способа приближенного решения уравнений:

Графическое решение.

Строят графики кривых у = j(х) и у = y(х); абсциссы точек пересечения кривых будут искомыми корнями данного уравнения. Далее пользуются методами для нахождения корней алгебраических уравнений.

2) Итерационный метод.

Пусть х = j(х) и y(х) = j(х).

а) графически или методом проб находят первое приближение корня

х = х0, х0 = первое приближение корня.

б) в правую часть уравнения х = j(х) подставим х0 и тогда х1 = j(х).

х1 - второе приближение корня.

в) подставляем в правую часть уравнения х = j(х) значение х1 вместо

х, х2 = j(х1), х2 – третье приближение корня.

г) таким образом, приближения получаются по следующей схеме:

х1 = j(х0);

х2 = j(х1);

х3 = j(х2);

х4 = j(х3) и т.д.

Важно отметить, что трансцендентное число можно представить при помощи числового ряда. Так, например в энциклопедии [29], сумма ряда 1 – 1/3 + 1/5 – 1/7 + 1/9 - … равна Õ/4; сумма ряда 1/12 +1/22 + 1/32 + ¼2 + … равна Õ2/6. Эти суммы дают возможность приближенно вычислить число Õ с любой, наперед заданной, степенью точности (если взять достаточно много членов ряда). Точность будем определять, пользуясь понятиями верных и значащих цифр.

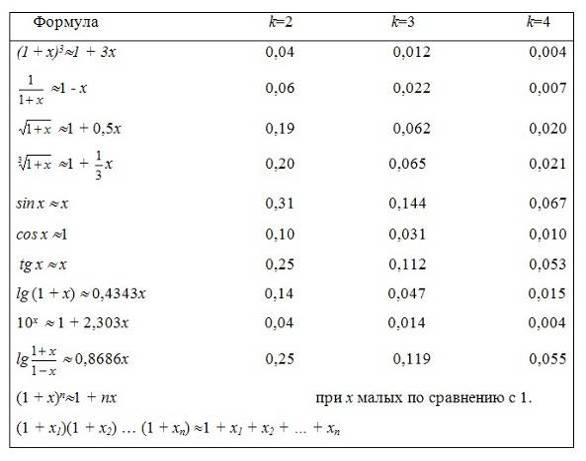
3. Приближенные формулы

Существует еще один раздел, тесно связанный с приближенными вычислениями - приближенные формулы. В энциклопедии приближенная формула определяется как “формула f(х)»f*(х), получаемая из формулы вида f(х) = f*(х) + e(х), где e(х) рассматривается как погрешность и после оценки отбрасывается”. Приближенные формулы позволяют при вычислении с приближенными числами быстро найти приближенный ответ. Приведем несколько наиболее употребительных приближенных формул, причем отметим, при каких ограничениях на |х| формула будет давать k точных десятичных знаков.

В приложении 1 к данной дипломной работе представлены графики функций, позволяющие увидеть, насколько близки друг к другу точные и приближенные корни уравнений.

В учебнике Башмакова М. И. представлены формулы для приближенных вычислений значений функции

f(x) – y0 » f/(x0)Dx; y » y0 + dy; у » у0 + f/(x0)(x – x0).

Применяя вышеперечисленные формулы можно построить несколько приближенных формул.

- Дана степенная функция у = хn. Зафиксируем точку х0 и применим формулу: (х0 + Dх)n » х0n + nx0n-1Dх.

- Дана функция у = .

Получаем приближенную формулу: » - .

4. Приближение функции

В БЭС приближение функций определяется как “нахождение для данной функции f функции g из некоторого определенного класса, в том или ином смысле близкой к f, дающей ее приближенное представление”. Задача о приближении функции – это задача о замене одних функций другими функциями. Эта задача постоянно возникает как в математике, так и в ее приложениях, т. к. существуют теоретические и прикладные потребности в ее решении.

Теоретические:

приближение функций является одним из мощных средств исследования свойств самих функций. Существует раздел комплексного анализа – приближение функций комплексного переменного – изучающий вопросы приближенного представления функций комплексного переменного посредством аналитических функций специальных классов. В БЭС отмечено, что теория приближений тесно связана с другими разделами комплексного анализа (теорией конформных отображений, интегральными представлениями). Многие теоремы, формулируемые в терминах теории приближений, являются, по существу, глубокими результатами о свойствах аналитических функций и природе аналитичности.

Прочее о педагогике:

Принципы организации внеклассной работы по иностранному языку
В основе функционирования системы внеклассной работы по иностранному языку лежит ряд принципов, определяющих содержание, формы, методы, направление педагогического воздействия на личность, характер связи отдельных элементов системы. Исследуя литературу по организации внеклассной работы разных автор ...

Способы оценивания уровня развития собственно силовых способностей у детей младшего школьного возраста
Для оценки максимальной силы у детей младшего школьного возраста. Легче и проще всего произвести замер максимальной силы у детей данного возраста при помощи различных динамометров. Динамическую силу у детей младшего школьного возраста измерять не рекомендуется, так как чтобы измерить максимальную д ...

Из истории педагогики
Каждое поколение людей решает три важнейшие задачи: во-первых, освоить опыт предыдущих поколений; во-вторых, обогатить и приумножить этот опыт; в-третьих, передать его следующему поколению. Общественный прогресс стал возможен лишь потому, что каждое новое поколение овладевало опытом предков, обогащ ...