Описание проведенных проверочных занятий

Класс был разбит на две группы, и с каждой группой занятие проходило отдельно. Ход занятия в обеих группах во многом совпадал.

1. В начале урока детям напомнили о том, что ранее на факультативе они решали задание, где нужно было показать следующее: “Сумма двух треугольных чисел равна гетеромекному числу”. Детям объяснили, что это не просто задание, а что это утверждение, которое может быть теоремой. На вопрос, что такое теорема дети затруднились ответить, и им пришлось напомнить о том, что теорема это утверждение которое справедливо для всех чисел (т.е. выполняется не только для каких-то конкретных чисел, а для любого взятого числа).

2. Поступило предложение, проверить, будет ли это утверждение являться теоремой.

а) Сначала показали, что это утверждение справедливо, на конкретных примерах (рис. 3.5., рис. 3.6.). Попутно вспомнили, какие числа являются треугольными, гетеромекными.

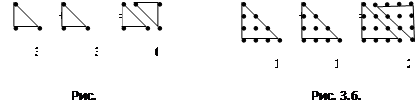
б) Далее перед детьми встал вопрос о том, как можно показать, что утверждение справедливо для всех треугольных чисел, ведь они сами выделили, что треугольных чисел бесконечно много и всех их перебрать нельзя. Поступило предложение о том, что нужно показать “любое” треугольное число (модель).

Строительством модели треугольного числа занимались все вместе.

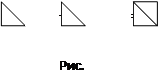
Первое, что предлагали дети, это показать форму треугольного числа (рис. 3.7.).

Затем предложили обозначить стороны за х (рис. 3.8.). На вопрос: “Почему именно х, а нельзя обозначить какой-то другой буквой?”, дети ответили: “Можно. Это буква обозначает, что сторона - любое число”.

Заметили, что получившаяся модель треугольного числа похожа на треугольник. Чтобы показать, что это треугольное число, а не треугольник выделили первый гномон-единицу (с чего начинается число) и последний (необходимо показать, что число состоит из гномонов) (рис. 3.9.).

Чтобы показать, что между первым и последним гномоном находятся еще гномоны (показать графически, что на стороне треугольного числа, х единиц), предложили расстояние между ними обозначить пунктиром. Было предложение еще посередине поставить гномон, но его посчитали неверным, т.к. это бы означало, что гномонов всего три.

Таким образом, была получена модель треугольного числа (рис 3.10.).

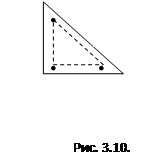
в) Используя полученную модель треугольного числа, пробовали доказать утверждение.

Во 2 группе ребенок, который работал на доске, получил квадратное число (рис. 3.11.).

Дети его исправили: “неправильно прибавил, он прибавил только уголок, а не все число”.

В итоге получили следующее (рис. 3.12.):

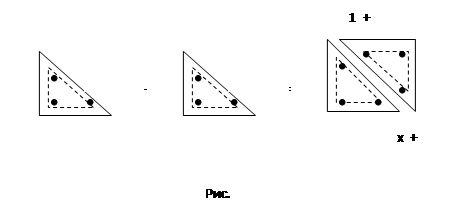
г) Определили, что у получившегося числа одна сторона равна х, а другая х и еще один гномон, т.е. х+1. На вопрос “Какое число получили?”, дети отвечали “Получили гетеромекное число, т.к. его стороны отличаются на единицу”.

Сделали вывод о том, что данное утверждение является теоремой, т.к. справедливо для всех треугольных чисел.

3. Дети сами сформулировали и записали теорему.

Прочее о педагогике:

Методика реализации программы кружка «Юный сказочник»
Занятие 1: « Знакомство» План занятия 1. Знакомство 2. Заполнение карточки «Мое имя» 3. Составление анкеты 4. Упражнение «Дотянись до потолка» Материалы: 20 карточек из белого картона 20 анкет Ход занятия 1) Знакомство. Преподаватель знакомится с детьми, представляется. На груди педагога - бейдж с ...

Понятие взаимодействия и характеристики продуктивного взаимодействия в образовательном процессе
В отечественной и зарубежной психологии всегда был актуальным поиск детерминант, определяющих характер взаимодействия в системе «педагог-обучаемый» и изучение его влияния на особенности развития личности. Сущностью процесса взаимодействия является непосредственное или опосредованное воздействие суб ...

Система мониторинга педагогической деятельности, реализуемая в ДОУ
Структура мониторинга и педагогической диагностики в ДОУ, этапы работы. I. Ориентационный этап: выбор проблемы, постановка цели. II. Диагностико-конструктивный этап: планирование диагностической деятельности, ее реализация, диагностическое прогнозирование. III. Обучающе-коррекционный этап: разработ ...