Описание проведенных проверочных занятий

1 группа: “Если любое треугольное число сложить с таким же треугольным числом, то получится гетеромекное число”.

2 группа: “Если любое треугольное число прибавить к тому же треугольному числу, то получится гетеромекное число”.

4. Далее детям было предложено проверить, будет ли являться теоремой следующее утверждение “Сумма двух последовательных треугольных чисел равна квадратному числу”. На вопрос “Вы можете это сделать?”, дети отвечали “да”.

Уч. Как?

Д. Построить модель, доказать на моделях, сформулировать теорему.

Уч. Модели, каких чисел нужно построить?

Д. Модели двух последовательных треугольных чисел.

Дети сразу определили, что у последующего треугольного числа стороны равны х+1 (отличаются на единицу) (рис. 3.13.).

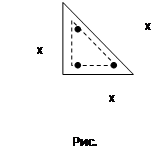
Используя полученные модели, доказали второе утверждение (рис. 3.14.).

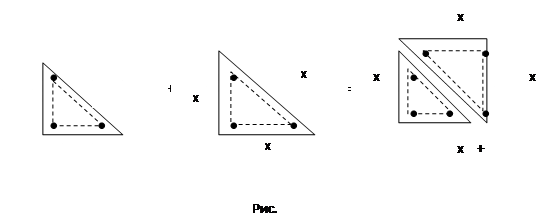
Определили, что у получившегося числа одна сторона равна х+1, другая х и еще один гномон, т.е. тоже х+1. Получили квадратное число, т.к. его стороны равны.

Сформулировали утверждение как теорему: ”Если любое треугольное число прибавить к следующему за ним треугольному числу, то получится квадратное число”.

Класс был разбит на две группы. С каждой группой занятие проходило отдельно. На занятиях принимали активное участие, в построении моделей фигурных чисел, в первой группе 6-7 человек из 12-14, а во второй группе 5-6 человек из 11-13.

Главная цель занятия состояла в том, чтобы проверить, способны ли дети моделировать на новом материале, там, где модель и объект моделирования существенно отличаются, а именно строить модели чисел представленных через эйдос. Задания подразумевали доказательства теорем, которые невозможны без построения моделей фигурных чисел, а также последующего выполнения действий с ними.

С построением моделей пифагорейских чисел, как в первой, так и во второй группе дети успешно справились. Дети смогли моделировать объекты фигурные числа, которые раньше никогда не моделировали и которые существенно отличаются своим видом от чисел представленных в РО.

При построении модели треугольного числа дети первое, что делали это, выделяли форму числа, а также предлагали обозначить сторону х. Это говорит о том, что дети могут переносить известные им элементы моделирования:

•обозначать неизвестное количество буквой, где буква - это любое число (говорят именно букву х, потому что видимо именно с ней работают на уроках математики; не отрицают, что можно обозначить любой другой буквой);

•обозначать пунктиром наличие гномонов находящихся между первым и последним.

С выполнением действий с моделями многие дети успешно справились, и когда во второй группе ученик на доске неправильно прибавил числа, его сразу поправили.

При исследовании полученного числа дети сразу увидели, что его стороны отличаются на единицу. На вопрос “Какое получилось число?” отвечали “гетеромекное”. В полученной, путем суммы двух треугольных чисел, модели гетеромекного числа наглядно было видно, какое это число.

После доказательства дети смогли сформулировать теорему, при этом, не забывая уточнять “любое треугольное число”.

Когда было предложено доказать еще одно утверждение стало ясно, что дети усвоили способ доказательства “нужно построить модель, доказать на моделях, сформулировать теорему”. При доказательстве второй теоремы сразу определили, модели каких чисел нужно строить, и что у модели последующего треугольного числа стороны будут равны х+1, т.к. он больше предыдущего на один гномон. Можно сказать, что у детей, получается, выстраивать способ работы с фигурными числами в “общем случае”.

Прочее о педагогике:

Рекомендации по формированию невербального общения
Если речь и связанное с ней вербальное общение умственно отсталого ребенка не развиты или развиты крайне пассивно, следует использовать невербальное общение. Роль невербальных средств общения с людьми, у которых имеются нарушения интеллекта, выступает с особой ясностью, так как неумение правильно в ...

Дидактические принципы лекционного занятия. Методы изложения лекционного материала
Дидактический принцип в обучении основан на том, что ознакомление студентов с каким-либо новым явлением или предметом начинается с конкретного ощущения и восприятия. Исследования показывают, что человек за счет зрения получает 70-80% всей информации, а лишь 20-30% за счет остальных органов чувств. ...

Общая характеристика развития речи детей раннего возраста
Ранний возраст является периодом, особенно благоприятным для освоения речи. Бурное развитие речи в дошкольном периоде связано с предметной деятельностью ребенка. На втором году жизни у ребенка возрастает интерес ко всему окружающему: он хочет все увидеть, познать, взять в руки. Эти желания превышаю ...